VII.

Linearum descendentium ab angulo cuiuslibet trianguli ad basim: quae angulum per aequalia dividit, minimam habet rationem ad mediam proportionalem inter basium segmenta; quae vero aequales hinc, et inde⁷¹ suscipiunt angulos, eamdem sortiuntur quoque⁷² rationem ad medias proportionales inter facta basium segmenta.

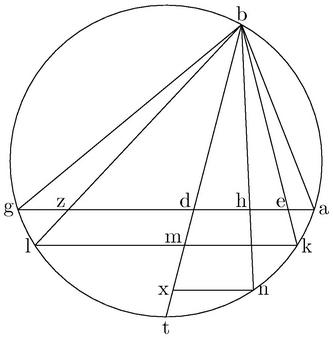
Sit triangulum ABG rectilineum; et ab angulo B ad basim AG descendant plures lineae; ex quibus ipsa BD secet angulum ABG per medium ipsae; autem BE, BZ suscipiant angulos ABE, GBZ, hinc inde aequales, ipsa⁷³ demum BH ipsis BD, BE intersit. Dico iam quod BD ad⁷⁴ mediam proportionalem inter segmenta AD, DG minorem habet rationem⁷⁵, quam BH ad mediam proportionalem inter AH, HG; et BH, ad mediam proportionalem inter AH HG minorem habet rationem, quam BE ad mediam proportionalem inter AE, EG; item quod BE ad mediam proportionalem inter AE, EG eamdem habet ratiooem⁷⁶ quam BZ⁷⁷ ad mediam proportionalem inter AZ, ZG. nam si trianguli⁷⁸ ABG latera AB, BG sint aequalia. tunc quoniam BD perpendiculariter⁷⁹ est ad basim; et perinde minima descendentium. Et⁸⁰ per 5. 2. Elementorum Euclidis, rectangulum ADG maximum est⁸¹ eorum, quae sub ipsius⁸² AG segmentis continentur; et perinde cum media proportionalis possit rectangulum sub segmentis contentum⁸³; media proportionalis inter AD, DG segmenta maxima sit mediarum⁸⁴ proportionalium inter segmenta sumptarum propterea iam BD ad talem mediam proportionalem minimam habebit rationem earum, quas habent descendentes ad medias proportionales factorum in basi segmentorum. item cum lineae BE, BZ sint aequales, ipsae⁸⁵ AE, ZG aequales; et perinde rectangulum AEG et⁸⁶ rectangulum AZG aequalia, et ob id mediae proportionales talium segmentorum aequales. iam et ipsae BE, BZ eamdem habebunt rationem ad ipsas medias proportionales. et eodem argumento BH ad mediam proportionalem inter AH, HG, minor erit proportio⁸⁷ quam BE ad mediam proportionalem inter AE, EG. quemadmodum proponitur demonstrandum.

Quod si trianguli⁸⁸ ABG latera AB, BG fuerint inaequalia; tunc per 5. 4. Euclidis, triangulo ABG circulus circumscribatur ABGLK; et ipsae BD, BE BZ, BH productae coincidant peripheriae apud t, k, l, n⁸⁹ puncta; coiniuncta⁹⁰ KL occurrat ipsi DT apud M; et ei aequidistans NX. eruntque arcus AK, LG aequales; quandoquidem aequos⁹¹ suscipiunt angulos: et ideo ipsae AG, [C:19v] KL, NX aequidistantes. quare per 2. 6. Euclidis, BH ad HN, sicut BD ad DX. maior autem est ratio⁹² BD ad⁹³ DX, quam BD ad DT⁹⁴. ergo maior est ratio⁹⁵ BH ad HN, quam BD ad DT⁹⁶. et propterea maior est ratio⁹⁷ BH ad mediam proportionalem inter BH, HN; quam⁹⁸ BD ad mediam proportionalem inter BD DT: quandoquidem si maior est dupla, quam dupla; maior est et simpla, quam simpla⁹⁹. verum media proportionalis inter BH HN est et media proportionalis inter AH, HG; quoniam rectangulum contentum sub his aequale est rectangulo contento sub illis per 34. 3. Euclidis: et similiter, media proportionalis inter BD, DT est ipsa media proportionalis inter AD, DG. igitur ratio¹⁰⁰ BH maior est¹⁰¹ ad mediam proportionalem inter AH, HG; quam BD ad mediam proportionalem inter AD, DG. item BD ad DM, hoc est BE ad EK est¹⁰² maior proportio¹⁰³, quam BD ad DX; hoc est BH ad BN¹⁰⁴; et [S:175] ideo BE ad¹⁰⁵ mediam proportionalem inter BE, EK; hoc est mediam proportionalem inter AE, EG maior erit¹⁰⁶ proportio¹⁰⁷ quam BH ad mediam proportionalem inter BH, HN; hoc est mediam proportionalem inter AH, HG. Denique sicut BE ad EK, sic BZ, ad ZL; utraque enim est¹⁰⁸ sicut BD ad DM. igitur sicut¹⁰⁹ BE ad mediam proportionalem inter BE, EK; hoc est mediam proportionalem inter A¹¹⁰E, EG; sic iam BZ ad mediam proportionalem inter bz, zl; hoc est mediam proportionalem inter¹¹¹ AZ ZG¹¹². Quae fuerant demonstranda.

Et manifestum fuit quod quadratum BD minorem habet rationem ad rectangulum ADG, quam quadratum BH ad rectangulum AHG. quodque quadratum BH minorem habet rationem ad rectangulum AHG, quam quadratum BE ad rectangulum AEG. quodque quadratum BE ad rectangulum AEG est¹¹³, sicut quadratum BZ ad rectangulum AZG. idemque dicendum si pro rectangulis segmentorum sumas quadrata mediarum proportionalium¹¹⁴.