VIII.

Ab angulo quolibet dati trianguli¹¹⁵ ad basim lineam rectam ducere; quae ad mediam proportionalem inter facta basis segmenta, datam habeat rationem. Oportet autem datam rationem non minorem esse ea, quam habet linea bifariam dividens angulum ipsum ad mediam proportionalem inter a se facta basis segmenta.

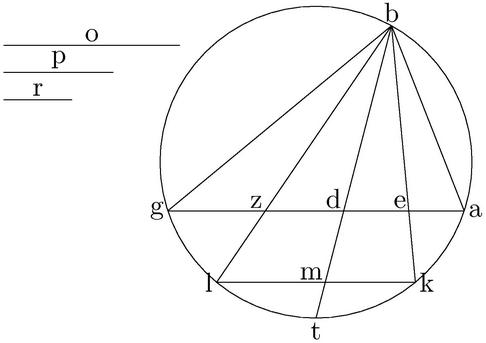
Sit datum triangulum ABG, in descriptione praemissae; data ratio, quam habet O linea ad lineam P. et oporteat ab angulo B ad basim AG rectam lineam ducere, quae ad mediam proportionalem inter basium¹¹⁶ facta segmenta [C:20r] rationem habeat, quam linea O ad lineam P. secetur per medium angulus ABG, ducta BD; et producta ad peripheriam ad punctum T; et sint ipsae O, P, R continuae proportionales. et si fuerit sicut¹¹⁷ O ad R, sic BD ad DT. iam tunc, fiet sicut O ad P, sic BD ad mediam proportionalem inter BD, DT; quae media proportionalis est inter AD, DG. et ideo in eo¹¹⁸ casu BD est linea, quam ductum iri voluimus. Si autem non fuerit sicut O ad R, sic BD ad DT, oportebit quidem maiorem esse proportionem¹¹⁹ O ad R, quam BD ad DT, ut maior sit ratio¹²⁰ O ad P, quam BD ad mediam proportionalem inter BD, DT; quae est media inter AD, DG. nam si minor¹²¹ esset ratio¹²² O ad P, quam BD ad mediam¹²³ inter AD, DG: problema non esset possibile; cum per praecedentem BD minimam habeat rationem earum, quam habent descendentes ab angulo B ad basim AG, ad mediam proportionalem inter facta basis segmenta. cum itaque¹²⁴ maior sit ratio¹²⁵ O ad P, quam BD ad mediam proportionalem inter BD, DT; vel inter AD, DG. maior utique erit ratio¹²⁶ O ad R, quam BD ad DT. sit ergo sicut O ad R, sic BD ad DM; et penes ipsam AG ducatur KML; et coniunctae KB, bl¹²⁷ coincidant ipsi AG, apud E, Z puncta. Dico igitur quod tam be¹²⁸ linea, quam BZ linea est, quae ducenda proponitur. nam cum per 2. 6. Euclidis, tam BE ad EK, quam BZ ad ZL sit sicut BD ad DM et perinde sicut O ad R. iam et tam BE ad mediam proportionalem inter¹²⁹ BE, EK; hoc est mediam inter AE, EG; quam BZ ad mediam inter BZ, ZL; hoc est mediam inter AZ, ZG, erit sicut O ad P mediam inter O, R. itaque tam BE, quam BZ est, quae¹³⁰ ducenda fuit.

Unde manifestum est, quod si data ratio fuit¹³¹ minima rationum, quas habent descendentes ab angulo B ad facta basis ag¹³² segmenta, tunc linea, quae ducenda proponitur, una tantum erit; ipsa videlicet BD bifariam secans angulum ABG. Si autem data ratio maior, quam minima fuerit, tunc semper geminae duci poterunt lineae, quales proponuntur; quae iam angulos hinc, et inde a linea BD, cum ipsa BD media, cumque lateribus trianguli suscipiunt aequales.[S:176]

SCHOLIUM.¹³³

Item quoniam duximus¹³⁴ ipsam BE ab angulo b¹³⁵ ad basim AG; estque sicut BE ad mediam proportionalem inter BE, EK; hoc est mediam inter AE, EG; sic O linea ad P lineam erit, et sicut quadratum¹³⁶ lineae O ad quadratum lineae P, sic quadratum BE ad quadratum dictae mediae hoc est ad rectangulum AEG. verum per 17. 6. Euclidis, sicut linea O ad lineam R, sic quadratum lineae [C:20v] O ad quadratum lineae P. igitur sicut linea O ad lineam R, sic quadratum BE ad rectangulum AEG. quamobrem si data sit ratio O ad R; et oporteat ducere ab angulo b¹³⁷ lineam ad basim AG, ita ut quadratum ductae ad rectangulum contentum sub segmentis basis sit, sicut O ad R. iam tunc linea, quam ducendam volumus¹³⁸, erit ipsa BE, sive BZ; sub tradito dudum praecepto comperta. idemque de linea BD, si data ratio O ad R sit, sicut quadratum BD ad rectangulum ADG; quae minima est rationum, quas habent quadrata descendentium ad rectangula¹³⁹ factorum in basi segmentorum hoc est ad quadrata mediarum¹⁴⁰ proportionalium inter ipsa segmenta: quandoquidem cum minima sit ratio laterum, inter rationes laterum. minima erit, et quadratorum ratio inter quadratorum rationes. unde tunc oportet datam rationem O ad R, non esse minorem ea, quam habet quadratum BD ad quadratum¹⁴¹ ADG, secus enim non esset possibile, quod proponitur faciendum.