IV.43
Ellipses, quarum transversae rectis diametris sunt proportionales: sunt inter se similes. contra similium ellipsium proportionales sunt transversae rectis diametris.
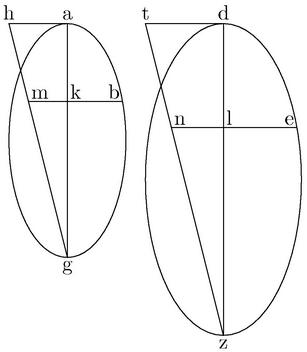
Sint duae ellipses ABG, DEZ, quarum transversae AG, DZ sint rectis diametris AH, DT proportionales. Aio quod similes sunt ABG, DEZ ellipses. Capiantur enim ex axibus segmenta ak, dl diametris proportionalia et ordinate ducantur bk, EL; quae productae ipsis GH, ZT coincidant apud m, n. quibus peractis, iam44 ut in praemissa, constabunt rectangula AKM, DLN similia in ratione duplicata eius, quam habet AK ad DL et quadrata BK EL in ratione duplicata eius [S:173] quam habet B45K ad EL. cumque per 13. primi Conicorum, quadratum BK aequum sit rectangulo AKM46; atque quadratum EL aequum sit rectangulo DLN, iam aequales erunt ipsae rationes duplicatae. quare et rationes ipsae aequales, hoc est BK ad EL47 Igitur axium segmenta diametris proportionalia, proportionales sibi ordinatas suscipiunt; idque48 idem in quibuscunque proportionalibus axium segmentis eveniet49 . itaque50 per diffinitionem similes sunt ABG DEZ51. Quod fuit demonstrandum.
Nec difficilius ostendetur conversa per ellipsim52 et aequam proportionem. Demum et hinc sequitur, ellipses, quarum transversae aequales, et rectae aequales: esse et53 inter se similes, et aequales. tunc enim cum tetragonae54, superficies quas possunt ordinatae sint aequales, erunt et ipsae ordinatae aequales. unde per diffinitionem, sectiones tunc similes, et aequales esse. Et e contrario.
Quod si ellipsium coniugatae diametri proportionales extiterint: non minus tunc ellipses inter se similes erunt. nam coniugatae diametri sunt mediae proportionales inter rectas diametros; et perinde supposita coniugatarum proportione, sequitur omnino rectarum ad ipsas proportio.[C:18v]