F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Photismi De Lumine et umbra Theorema 9
<- App. -> <- = ->

THEOREMA IX

24 Possibile est trianguli non aequilateri60, umbram aequilateram proiici.

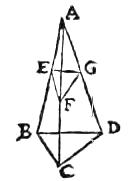
figura 11

25 Construatur enim pyramis ABCD, supra triangulum aequilaterum BCD, seceturque pyramis ipsa plano ad basim obliquo, quod sit EFG. Eritque iam EFG triangulum non aequilaterum. Si ergo intelligatur triangulum ipsum EFG a signo A illuminari, proiiciet iam umbram BCD, quae61 fuit triangulum aequilaterum. Quod erat demonstrandum.

Corollarium

26 Similiter igitur possibile est a qualibet non aequilatera figura umbram proiici aequilateram.[C:6r]62

Inizio della pagina
 ->