Theorema XVIII

Parallelorum radiorum intra perspicuum orbem a centro inaequaliter distantium remotior cum axe sibi parallelo propius sphaerae concurret, quam reliquus.

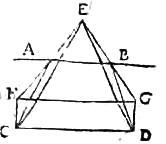
47 Intra sphaeram abd sint radii ab, cd, quorum ab sit a centro remotior, qui egredientes frangantur in b, d signis. Dico²⁹⁸ quod ab cum diametro ef sibi parallelo in signo g²⁹⁹ concurret sphaerae propinquiori ipso h signo in³⁰⁰ quo ab³⁰¹ fractus cum eadem diametro concurrit. Sit enim sphaerae centrum k, et connectantur³⁰² bk et dk et³⁰³ concurrat, si possibile est, [A:5v] ab radius fractus ad signum h, connexa bh et³⁰⁴ protrahatur in rectum hd ad circumferentiam ad signum l, et connectantur³⁰⁵ bl et lf. 48 Et, quoniam in triangulo lfh portio basis hd³⁰⁶ non est minor latere hf, ideo (sicut Ptolemaeus³⁰⁷ in [S:42] quodam lemmate 12ⁱ³⁰⁸ voluminis suae magnae Constructionis³⁰⁹ demonstrat) maior erit³¹⁰ proportio hd ad dl quam anguli dlf³¹¹ ad angulum fhd. Et conversim minor proportio lineae ld ad lineam dh quam anguli fhd³¹² ad angulum dlf³¹³.

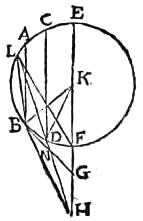
49 Et³¹⁴ quia etiam in triangulo lbh portio³¹⁵ basis ld non est minor latere lb, ideo maior est proportio lineae ld ad lineam dh quam anguli bhd³¹⁶ ad angulum bld. Quare multo magis maior fiet proportio anguli fhd ad angulum dlf³¹⁷ quam proportio³¹⁸ anguli bhd ad angulum bld. Sed angulus dlf³¹⁹ dimidium est ipsius anguli dkf, et angulus bld 1/2³²⁰ est ipsius anguli bkd. Ergo³²¹ sequitur, per aequam³²² proportionalitatem, ut maior sit proportio anguli fhd ad angulum dkf quam anguli³²³ bhd ad angulum bkd. Et permutatim maior sit angulus fhd ad angulum bhd quam angulus dkf ad angulum bkd. 50 Et³²⁴ conversim angulus bkd maior sit ad angulum dkf quam angulus bhd ad angulum fhd 51 et coniunctim maior sit angulus bkf ad angulum dkf quam angulus bhf ad angulum dhf.³²⁵ Sed³²⁶ anguli bkf et dkf³²⁷ propter linearum aequidistantiam³²⁸, sunt angulis abk³²⁹ et cdk³³⁰, qui³³¹ a perpendicularibus et fractis³³² comprehenduntur³³³, aequales, ipsi vero anguli bhf et dhf sunt fractionum angulis, eadem ratione, aequales. 52 Igitur anguli, qui sub perpendicularibus et fractis³³⁴ comprehenduntur, non erunt fractionum angulis proportionales. Quod est contra 10^am335 huius libelli. Non igitur ab fractus ad signum h ipsi ef diametro concurret. Sed neque inferius; tunc enim angulus fractionis, qui esset ipse bhf, si ab ad signum h frangeretur, minor quam bhf³³⁶ fieret, et tunc³³⁷ multo fortius angulus bkf ad angulum dkf maior esset quam angulus fractionis radii ab ad angulum dhf. 53 Superest ergo ut ab fractus ad aliquod³³⁸ signum propius sphaerae quam h ipsi diametro ef congrediatur, quod sit g signum, secetque³³⁹ ipsum dh in m signo³⁴⁰.

Corollarium

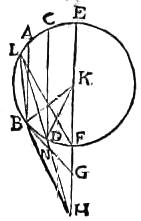
Sequitur ergo ut, quotlibet parallelis radiis per sphaeram perspicuam vagantibus, semper remotior a centro, vicinius ad sphaeram,³⁴¹ diametrum³⁴², qui³⁴³ ex parallelis est, occurrat³⁴⁴, ac ante occursum secet centro propiorem et vicissim secetur a remotiori. [S:43]