[A:15v] ELEMENTORUM SEXTUS

1 Similes figurae sunt, quorum anguli numero et magnitudine singuli singulis aequales, et opposita eorum latera proportionalia.

Reciproca triangula, seu parallelogramma, sunt quorum latera circum aequos angulos sunt in reciproca ratione. Seu mutuo proportionales.

Propositiones

p^a

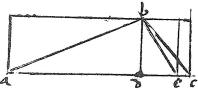
2 Parallelogramma, vel triangula eiusdem altitudinis sunt proportionalia basibus.

Sit parallelogramma abbc eiusdem altitudinis super bases ad, dc. Aio quod sicut est basis ad  basim dc sic  ab   bc. 3 Nam si bases sunt commensurabiles, erunt per p^am quinti, sicut numeri, et earum ratio denominata a numeris. Et tunc eiusdem nominis erit ratio parallelogrammorum per 36^am primi, divisis basibus in partes aequales communi mensurae, et parallelogrammis in totidem partes. 4 Si autem bases non sint in ratione nominata, tunc sit ratio nominata quaevis ad  de ut scilicet sit minor ratio ad  dc quam ratio ad  de. Et tunc minor erit ratio  ab   bc quam ratio  ab   be, eiusdem nominis, cum nomine basium ad, de. Et similiter ostendemus, quod quacumque ratione nominata minor erit ratio basis ad  basim dc hac eadem minor erit ratio  ab   bc et qualicumque maior: maior. 5 Igitur per conversionem diffinitionis rationum¹ aequalium, erit ratio basis adbasim dc sicut ratio   ab   bc. Hoc idem de triangulis sequitur, quae sunt dimidia parallelogrammorum. Sicut proponitur demonstrandum.

[A:16r]

2^a

6 Recta basi trigonico parallelus, in reliquis lateribus proportionalia facit segmenta. Et e contrario.

In triangulo abc linea de sit basi ac parallelus. Dico tunc quod sicut est bd  da sic be  ec. Iungantur enim rectae cd  ae eruntque, per 36^am primi triangula aed, cde invicem aequalia. 7 Et ideo erit sicut  bde  ^lum cde sic ^lum bde  ^lum aed per 2^am conceptionem quinti. Sed per praecedentem ^lum  bde  ^lum cde sicut be  ec. Et ^lum bde  ^lum aed sicut bd  da. Ergo per 6^am conceptionem quinti bd  da, sicut be  ec. Quod est propositum.

8 Contra si sit bd  da sicut be  ec tunc ipsa de ipsi ac parallelus erit. Nam tunc, per praemissam, ^lum bde  ^lum aed sicut ^lum bde  ^lum cde quare per 2^am conceptionem 5ⁱ triangula aed, cde aequalis. Et ideo per 39^am pⁱ de parallelus ipsi ac quod est reliquum.

3^a

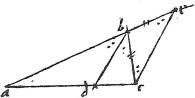
9 Recta secans angulum trianguli per aequalia, secat basim in portiones conterminis lateribus proportionales. Et e contrario.

Ut si trianguli abc angulum b linea bd secet in angulos abd, dbc aequales. Dico quod sicut ab  bc sic est ad  dc. Ducatur enim ipsi bd parallelus ce; cui occurrat ab continuata ad punctum e. 10 Eruntque propter aequidistantiam linearum anguli abd et e aequales, et anguli dbc, bce aequales quare anguli bce et e aequales et perinde latera eb, bc aequalia. Sed per praemissam ab  be sicut ad  dc. Igitur ab  bc sicut ad  dc quod est propositum. Contra ex aequalitate linearum be, bc concludes per praemissam, lineas bd, ec parallelos et aequalitatem angulorum.

[A:16v]

4^a

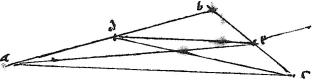
11 Triangulorum invicem aequiangularum latera aequos angulos subtendentia sunt proportionalia. Et e contrario.

Ut si triangulum abc triangulo dbe sit aequiangulum: ex aequalitate angulorum sequitur aequidistantia basium de, ac et proportio laterum ex 2^a huius. 12 Et ducta df parallelo ad, bc sequitur eadem ratio inter ac, cf et ideo inter ac, de. Contra ex proportione laterum sequitur aequidistantia, et aequalitas angulorum.

Corollarium

13 Ex hac manifestum est, quod duo triangula aequiangula invicem sunt similia. Et quod omnes duae figurae similes sunt divisibiles in triangula eiusdem numeri singula singulis similia.

5^a

14 Cathetus ab angulo recto trianguli orthogoni est media proportionalis inter portiones basis: et secat triangulum in duo triangula, invicem et toti similia triangulo. Et laterum utrumque medium proportionale est inter basim et sibi conterminatam basis portionem.

15 Nam ex aequalitate angulorum² sequitur per praecedentem proportio laterum et similitudo triangulorum. Et talis continua proportio linearum. Tale autem triangulum in semicirculo continetur per 30^am tertii. Sic triangula abc, adb, bdc similia. Lineae ad, db, dc proportionales; lineae da, ab, ac proportionales. Item dc, cb, ca proportionales.

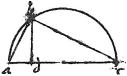
Corollarium

16 Hinc ergo, cum dantur ex tribus lineis proportionalibus duae tantum: invenietur reliqua.

6^a

In triangulo orthogonio, si super tria latera singulae figurae similes ac similiter describantur; figura super maximum latus descripta aequalis erit reliquis duabus simul sumptis.

17 Si agas de triangulis orthogoniis, constat propositio in praecedentis lineamento. Ubi triangulum abc super ac latus maximum locatur, et iam triangulis adb, bdc similibus similiterque locatis, ac [A:17r] simul sumptis aequale est. Sic ergo tria alia triangula, sive tria quadrilatera, sive tria pentagona, aut poligona similia, similiterque super singula trianguli abc latera si constituantur, (quoniam eandem semper inter se proportionem, scilicet duplam laterum respondentium servant) hanc eandem colligantiam tenebunt, ut figura super latus ac³ posita aequivaleat aggregatum figurarum super latera ab, bc positarum. 18 Quod etiam de circulis, et eorum similibus portionibus verificatur. Nam circuli et similes eorum portiones sunt quadratis ac similibus rectilineis proportionales.

7^a

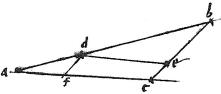
Datam lineam, secundum proportionem partium lineae divisae secare.

19 Esto in triangulo abc data linea ab divisa vero bc in puncto e. Ducatur ipsi ac parallelus ed eritque per 2^am sicut bd  da sic be  ec quod est propositum. Similiter si linea bc plurifariam sive aequaliter, sive secus secetur, semper lineae per divisionum puncta, ipsi ac paralleli, ad eandem proportionem secabunt ipsam ab sicut proponitur. 20 Hinc ergo tribus lineis datis quarta proportionalis subiungetur. Et data linea in quotlibet aequales partes secabitur.

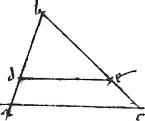
8^a

Eundem, sive aequalem angulum habentium triangulorum ratio ex rationibus laterum talem angulum complectentium componitur.

21 Ut si triangula abc, dbe angulos apud oppositos habeant aequales. Coniuncta cd iam ratio ^li abc  ^lum dbe componitur ex rationibus ^li abc  ^lum  cbd⁴ et ^li bcd  ^lum dbe. Et ideo ex rationibus ab  bd et cb  be quia per p^am triangula sunt basibus proportionalia. Sic constat propositum.

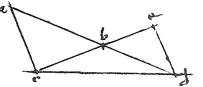
9^a

22 Eundem sive aequalem angulum habentium parallelogrammorum ratio ex rationibus laterum an[A:17v]gulum aequalem complectentium componit.

Sequitur ex praecedenti: nam dimidia parallelogrammorum sunt triangula quorum ratio ex rationibus dictorum laterum componitur et ideo ratio parallelogrammorum ex iisdem. 23 Hic manifestum est, quod similium triangulorum ratio est sicut respondentium laterum ratio duplicata. Et quod similium figurarum (quoniam in similia et totidem triangula distinguuntur) ratio est sicut respondentium laterum ratio duplicata. 24 Item quod reciproca triangula sunt invicem aequalia et reciproca parallelogramma invicem aequalia. Et e contrario. Item ex hac reciprocorum parallelogrammorum aequalitate sequitur quod in quatuor lineis proportionalibus, quod sub extremis, aequale est ei, quod sub mediis comprehenditur rectangulo. Contra et si rectangula talia fuerint aequalia, lineae proportionales erunt. 25 Item ex hoc postremo corollario sequitur, quod in tribus lineis proportionis continuae, quod sub extremis rectangulum aequum esse mediae quadrato. Contra, ut haec productorum aequalitas arguat linearum proportionem. Quarum demonstratio in hoc nono theoremate patet. Sic paucis cuncta necessaria complexi sumus.

10^a

26 Duobus quibuscumque datis rectilineis duas rectas proportionales invenire.

Super aliquam ad libitum positam lineam constituatur parallelogramma continuatim singula triangulis in quae distinguitur utrumque rectilineum, aequalia: et hoc per 44^am primi. 27 Nam parallelogramma singulis rectilineis aequalia, per p^am huius, et ideo ipsa rectilinea erunt comparatis basibus proportionalia. Bases ergo erunt quaesite recte.

11^a

Duobus propositis rectilineis, figuram uni eorum aequalem et alteri similem describere.

28 Proponatur exempli gratia triangulum a et pentagonum b cuius latus c ut iam oporteat designare pentagonum triangulo a aequale, et [A:18r] pentagono b simile. Ponatur per praecedentem, sicut⁵ ratio pentagoni b  triangulum a sic ratio lineae c  lineam d. 29 Et ipsis c, d lineis intersit per 5^am. huius media proportionalis e super quam constituatur similis et similiter locata figura ipsi b hoc est pentagona, et aequiangula et proportionalium laterum ipsi b pentagono quae sit f. Dico igitur tunc quod f pentagonum aequale est triangulo a et simile pentagono b. 30 Cum enim lineae ced sunt continue proportionales: fiet ratio c  d duplex rationis c  e scilicet figura b  figuram f duplicem habet rationem c  e per corollarium nonae huius. Ergo per conceptionem 6^am quinti sicut figura b  figuram f sic linea c  lineam d fuit autem c  d sicut pentagonum b  ^lum a. 31 Ergo per dictam conceptionem sicut pentagonumb  ^lum a sic figura b  figuram f. Eandem ergo rationem pentagonum b  figuram f et  ^lum a. Quare per p^am conceptionem quinti figura f aequalis est triangulo a fuitque similis pentagono b. Ipsa est igitur quaesita.

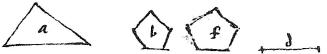
32 Illud autem nota, quod quando duarum similium figurarum duos quaevis respondentia latera in una sunt recta, sive aequidistant; tunc bina quaeque latera respondentia ex reliquis sunt aequidistantia, et quoque in una recta. Et dicuntur tunc figurae similes ac similiter positae.

12^a

33 Datam lineam secundum extremam mediamque rationem secare.

Esto data linea ab secetur per 11^am 2ⁱ in puncto c Ita ut rectangulum ab bc aequum sit quadrato ca tunc enim, per postremum corollarium 9^e lineae ba, ac, cb sunt in proportione continua. Et sic proponitur linea secanda.

13^a

34 Anguli sive ad centra, sive ad circumferentias circulorum aequalium constituti sunt assumptis arcubus atque sectoribus circulorum proportionales.

35 Nam si anguli sunt com[A:18v]mensurabiles, tunc per 25^am et 26^am tertii, et arcus assumpti tam ad centrum, quam ad periferiam positi erunt secundum eosdem numeros commensurabiles: quare quoties communis mensura metitur angulum, toties et communis mensura metitur arcus et communis mensura sectores. 36 Unde per diffinitionem tunc tam ratio angulorum, quam arcuum, et quam sectorum cadet sub eorundem numerorum appellationem: et eiusdem nominis erit. 37 Quod si anguli fuerint incommensurabiles, tunc quacumque ratione nominata minor fuerit ratio angulorum: hac eadem minor erit et ratio assumptorum arcuum, et ratio sectorum. Et quacumque illa maior, haec et maior. 38 Quare rursus per diffinitionem, anguli sive ad periferiam, sive ad centrum constituti, tam assumptis arcubus, quam sectoribus proportionales erunt. Sicut demonstrandum proponitur.

9 februarii

14^a

39 Cum duae rectae se invicem intra circulum secant: rectangula sub singularum portionibus contenta sunt inter se aequalia.

Nam anguli per 26^am 3ⁱ aequales faciunt triangula similia. Unde per 4^am et tertium corollarium nonae sexti: constat propositum.

15^a

40 Duabus rectis lineis ab uno puncto eductis, una tangente, altera secante circulum: rectangulum, quod sub secante et eius extrinseca portione continetur, aequale est ei, quod a tangente fit quadrato.

41 Nam adducta 31^a tertii, anguli aequales facient triangula similia. Unde per 4^am et quartum corollarium 9^e sexti sequitur propositum.

Quamvis hae duae in fine tertii fuerint demonstratae. Hic tamen ex similitudine triangulorum facilius concluduntur.

Corollarium

42 Unde talia duarum rectarum ab uno puncto circulum secantium rectangula semper inter se aequalia esse necesse est.

Scholium

Similiter, ingeniose lector, in sexta sexti per similitudinem triangulorum facilius et universalius ostendebatur penultima primi. 43 Non solum scilicet de quadratis, sed de quibuscumque similibus ac similiter positis figuris.

26 octobris 1567