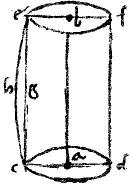
2a Si cylindrus plano secetur per axem: sectio parallelogrammum est.
Sit cylindrus cuius bases, qui circum a b centra circuli; axis autem ab per quem producatur planum secans cylindrum, sitque sectio cdfe.
Aio sectionem cdfe parallelogrammum esse.
Nam per 3am 11i ipsae ef cd erunt rectae, et per 16am eiusdem paralleli, et etiam aequales quoniam aequalium circulorum diametri.
Sed et ipsae cge2 df in cylindrica superficie rectae quoque sunt.
Nam si egc non sit recta, ducatur ergo recta che quae erit extra cylindri superficiem.
Sed ipsae ac be iampridem paralleli et aequales circumactae et che rectam circumferentes describent cylindrum per diffinitionem namque ipsae ac be circulos, ipsa vero che cylindricam superficiem describunt.
Itaque che ibit per cylindricam superficiem atque erat extra quod est impossibile. Recta ergo est linea cge similiter et ipsa df fuerunt at ipsae cd ef aequales et paralleli; ergo per 33amprimi ipsae ce df aequales et paralleli: quare cefd parallelogrammum; quod est propositum.
Corollarium
Et manifestum est quod si cylindrus rectus est, parallelogrammum per axem semper rectum est ad basim: si autem scalenus, parallelogrammum per axem3 non semper rectum est ad basim.