F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis liber de sphaera et cylindro 17
<- App. -> <- = ->

PROPOSITIO XVII.

Si sphaera plano secetur segmentorum sphaericae superficies sunt ad invicem sicut axes segmentorum.

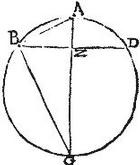
figura 20

Repetens proximae descriptionem; aio quod superficies sphaerica segmenti BAD ad superficiem sphaericam segmenti BGD, est sicut axis AZ ad axem ZG. Nam per 8. sexti ratio AZ ad ZG dupla est eius, quae AZ ad ZB: sicut AZ ad ZB, sic AB ad BG (propter similitudinem triangulorum AZB ABG.) Ergo ratio AZ ad ZG dupla est eius, quae AB ad BG, et eius, quae AB ad BG dupla est per 18. sexti ratio quadrati AB ad quadratum BG: quare, quadratum AB ad quadratum BG, sicut AZ ad ZG: sed ex 2.12. circulus, cuius semidiameter AB ad circulum, cuius semidiameter BG, sicut quadratum ex duplo AB ad quadratum ex duplo BG; et ideo sicut quadratum AB ad quadratum BG: igitur circulus, cuius semidiameter AB ad circulum, cuius semidiameter BG, sicut AZ ad ZG. Verum circulus, cuius semidiameter AB aequalis est per praemissae corollarium. sphaericae superficiei segmenti BAD: ergo sphaerica superficies segmenti BAD ad sphaericam superficiem segmenti BDG est sicut axis AZ ad axem ZG: quod est propositum.

COROLLARIUM.

Manifestum est ergo quod sphaerae superficies ad sui segmenti sphaericam superficiem est sicut diameter sphaerae ad axem segmenti patet ex coniuncta proportione.

Inizio della pagina
 ->