F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de momentis aequalibus Liber tertius 24
<- App. -> <- = ->

PROPOSITIO XXIV.

Si in sectione conica, quae parabolae vocatur, triangulum super eandem basim, et eandem diametrum inscribatur: diameter eius quadrupla erit ad diametrum tam unius, quam alterius relictarum portionum: quadrupla item ad sui segmentum a vertice ad lineam, quae coniungit vertices portionum.

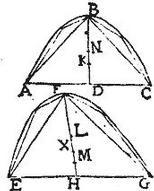
figura 25

In parabola ABC, cuius diameter BD, basisque AC, inscriptum sit triangulum ABC super eandem basim, eandemque diametrum, sectisque bifariam AB, BC in punctis F, G: ducantur relictarum portionum diametri KF, LG, et coniuncta KL secet diametrum BD in puncto S. Demonstrandum utique est, quod BD quadrupla est tam ipsius KF, quam ipsius LG, quamque ipsius BS. Hoc modo per 20. primi conicorum elementorum, sicut BD ad [S:152] BS, sic quadratum AD ad quadratum KS.

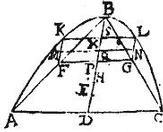
figura 26

Coniungatur FG secans ipsam BD apud P punctum: aequidistabit autem KL ipsi AC per 15. huius, et FG aequidistabit iisdem per 2. sexti Euclidis. Quare FP aequalis ipsi KS. Igitur sicut DB ad BS, sic quadratum AD ad quadratum FP: sed quadratum AD quadruplum est ipsius quadrati FP: quandoquidem AD dupla est ipsius FP, sicut AB dupla ipsius FB: ergo quadrupla est DB ipsius BS: cumque BP sit dimidium ipsius BD; quando FB dimidium est ipsius BA: iam SP et ipsi aequalis tam KF, quam LG aequalis erit ipsi BS. Quamobrem et ipsa BD quadrupla erit ipsius tam KF, quam LG: sicut proponitur demonstrandum.

Inizio della pagina
 ->