PROPOSITIO XIX.
Si tres lineae tribus lateribus trianguli cuiuslibet aequidistantes ducantur ita secantes latera singula, ut portio ad angulum subsectis contentum recepta dupla sit reliquae; ductae se per aequalia vicissim et super uno puncto divident, quod est trianguli centrum.
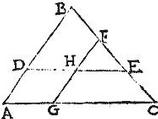
In triangulo ABC duabus lineis DE, FG, quae lateribus CA, AB aequidistantes sic secant latera, ut proponitur; superveniat tertia linea KL aequidistans tertio lateri BC, et similiter secans latera AB, AC in punctis K, L: aio quod KL per punctum H ibit, omnesque tres per aequalia in H puncto, quod trianguli ABC centrum est, sese dispescent: namque per 16. huius, ipsarum DE, FG utraque alteram per aequalia secat, et per eandem KL per aequalia secabit ipsam DE ipsamque FG, et perinde per punctum H ibit, et per 17. vicissim per aequalia secabitur ab eis in puncto H: omnes igitur tres lineae DE, FG, KL se vicissim per aequalia secant in puncto H: et per praecedentem, ipsum H punctum centrum gravitatis trianguli ABC existit: quemadmodum proponebatur demonstrandum.