PROPOSITIO XXVIII.
Si gravia reciproca sint distantiis, quibus absunt centra ipsorum a puncto quodam in recta linea coniungente centra posito; punctum illud est commune centrum gravium.
Ponatur ut prius duo inaequalia gravia A, B, sitque C punctum quoddam in linea AB, ut faciat segmenta ordine permutato proportionalia gravibus; hoc, est ut sicut grave A ad grave B, sic sit distantia BC ad distantiam CA: dico iam quod punctum C est commune centrum gravium A, B: fiant enim ea omnia, quae in praecedenti: eritque similiter sicut BC linea ad CA lineam, et ideo sicut A grave ad B grave, sic iam GK grave ad KH grave: et perinde cum totum GH grave positum sit aequale toti AB gravi: erunt singula singulis aequalia, hoc est grave GK aequale gravi A, atque grave KH aequale gravi B: cumque per 25. huius, totius GH gravis uniformis centrum sit F; et centra segmentorum GK, KH sint D, E; iam per 10. huius, gravia GK, KH aequeponderabunt a puncto F, hoc est ad spatia DF, FE: verum gravia A, B ipsis gravibus GK, KH singula singulis sunt aequalia; et spatia AC, CB eadem ipsis DF, FE spatiis. Igitur per 5. postulatum, A, B pondera aequeponderabunt ad AC, CB spatia a puncto scilicet C suspensa. Quare per 11. huius, C commune centrum est ipsorum A, B gravium: quod erat demonstrandum.
Idem, et aliter demonstrabitur ab impossibile per praecedentem; hoc modo. [S:100]
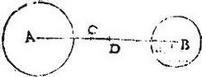
Sint A, B gravia inaequalia, sitque in ipsa AB linea punctum C, itaut sicut est A ad B, grave scilicet ad grave, sic sit BC, ad CA spatium ad spatium. Aio quod C punctum est commune centrum ipsorum A, B gravium: nam si possibile est, sit ipsorum A, B gravium commune centrum aliud, quam C punctum, sitque illud D; eritque per praecedentem, sicut A grave ad B grave, sic BD spatium ad DA spatium: sed per hypothesim, sicut A grave ad B grave, sic BC spatium, ad CA spatium, igitur sicut BC spatium ad CA spatium: sic BD spatium ad DA spatium; et coniunctim sicut AB spatium CA spatium, sic AB spatium ad DA spatium: igitur spatia DA, AC sunt aequalia, quod est impossibile: non est ergo commune ipsorum A, B gravium centrum aliud quam C punctum: quod fuit demonstrandum.