http://WWW.dm.unipi.it/didactics/home.html
Elementi di Analisi Matematica II, Anno Accademico 2002-2003, Matematica
http://WWW.dm.unipi.it/didactics/home.html
![]() El. di An. Mat. I e II A.A. 2002/03
El. di An. Mat. I e II A.A. 2002/03
-------------------------------------------------------------
ESERCIZIO n. 1
a - Si studi la convergenza delle seguenti serie:
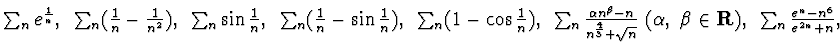
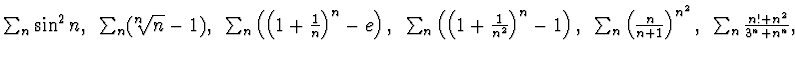
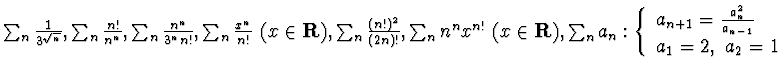
![]()
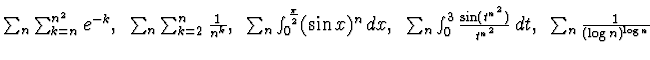
b - Stabilre se i seguenti integrali generalizzati sono convergenti:
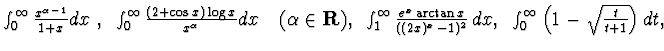
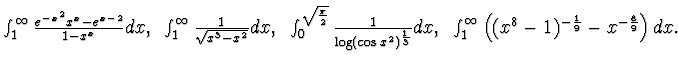
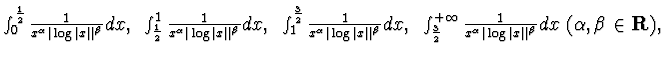
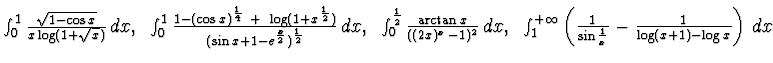
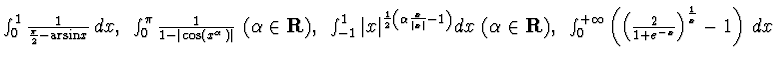
-------------------------------------------------------------
ESERCIZIO n. 2
a - Si provi che le serie di Taylor di centro 0 di
![]() è convergente alla funzione stessa per
è convergente alla funzione stessa per
![]() .
.
b - Si provi che le serie di Taylor di centro 0 delle funzioni
![]() sono assolutamente convergenti per ogni
sono assolutamente convergenti per ogni
![]() ,
e
quindi che rispettivamente convergono alle funzioni di cui sono sviluppo.
,
e
quindi che rispettivamente convergono alle funzioni di cui sono sviluppo.
c - Si provi che il resto dello sviluppo di Taylor in 0 di grado 2n+2della funzione
![]() è in modulo minore di
è in modulo minore di
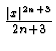 .
(Per esempio si può usare la serie gometrica di ragione
-x2).
.
(Per esempio si può usare la serie gometrica di ragione
-x2).
d - Si trovi una funzione la cui serie di Taylor in 0 converge per ogni
![]() ,
ma non converge alla funzione stessa.
,
ma non converge alla funzione stessa.
-------------------------------------------------------------
ESERCIZIO n. 3* Si pone
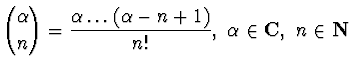 .
Si calcoli lo sviluppo di Taylor
in 0 della funzione
.
Si calcoli lo sviluppo di Taylor
in 0 della funzione
![]() e si provi che
converge alla funzione stessa per
e si provi che
converge alla funzione stessa per
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 4 Si ocnsideri
![]() .
.
a - Si provi che tale funzine può essere estesa con continuità a tutto
![]() .
.
b*- Si studi la derivabiltà di tale estensione.
-------------------------------------------------------------
ESERCIZIO n. 5
Posto
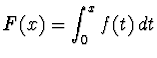 ,
si studi il limite del rapporto
,
si studi il limite del rapporto
![]() ,
,
![]() ,
nei seguenti casi:
,
nei seguenti casi:
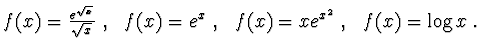
-------------------------------------------------------------
ESERCIZIO n. 4 Sia
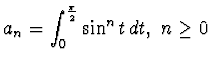 .
.
a - Si provi che
![]() e quindi
e quindi
![]() ,
,
![]() .
.
b - Si deduca che
![]() [Formula di
Wallis].
[Formula di
Wallis].
-------------------------------------------------------------
ESERCIZIO n. 5
a - Si provi che
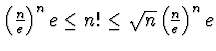 ,
valutando
,
valutando
![]() .
.
b - Si provi che
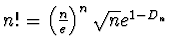 ,
si dia
un interpretazione geometrica alla successione Dn mostrando tra l'altro che è
crescente.
,
si dia
un interpretazione geometrica alla successione Dn mostrando tra l'altro che è
crescente.
c - Detto D il limite di Dn si provi che
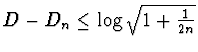 .
.
d - Usando la formula di Wallis si provi che
![]() e
quindi la formula di Stirling
e
quindi la formula di Stirling
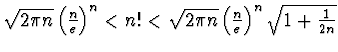 .
.
-------------------------------------------------------------
ESERCIZIO n. 6
a - Si consideri
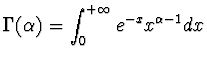 ,
,
![]() .
Si provi che è ben definito e quindi che
.
Si provi che è ben definito e quindi che
![]() per
per
![]() .
.
b - Sia
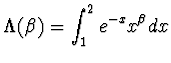 ,
,
![]() .
Si provi che è
derivabile con derivata eguale a
.
Si provi che è
derivabile con derivata eguale a
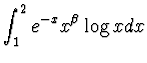 .
.
c - Si studi il caso
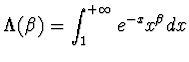 .
.
-------------------------------------------------------------
ESERCIZIO n. 7 Si considerino gli integrali
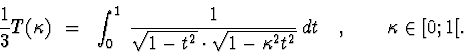
a) Si calcoli T(0) e si provi che per ogni
![]() tali integrali sono finiti.
tali integrali sono finiti.
b) Si studi al variare di
![]() il comportamento di
il comportamento di
![]() per
per
![]() .
.
-------------------------------------------------------------
ESERCIZIO n. 8
questioni numeriche
funzioni continue mai derivabili
insiemi di cantor
funzioni definite con integrali o serie
serie di errori di successioni definite per ricorrenza
-------------------------------------------------------------
ESERCIZIO n. 9