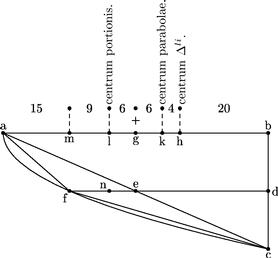
Brevis demonstratio centri in parabola
1 afc parabola cuius diameter ab. Basis bc. abc triangulum ad quod parabola sesquitertia est. Unde afc portio tertia pars est trianguli abc. 2 Item divisa bc per aequalia in puncto d erit ipsi ab aequidistans def diameter portionis. g punctum medium in diametro. bh sit ipsius ha dimidium. Eritque h centrum trianguli abc. bk sit 2/3 ipsius ka. Eritque k centrum parabolae. 3 Item divisa ga per aequalia in puncto m erit ipsa gm aequalis ipsi ef. Igitur esto gl 2/3 ipsius lm. Eritque l centrum portionis dictae. Sed centrum intellige punctum a quo spacium suspensum in libra ab perpendiculariter demittit ipsum gravitatis centrum
4 Consydera igitur in libra hkl triangulum abc pendere ad spacium kh. Et portionem afce pendere ad spatium kl. Et iam spatia reciproca sunt ponderibus quoniam hk tertia pars est ipsius kl. Et portio tertia pars trianguli.
5 Item sicut in diametro ab parabolae abcf linea bk est 2/3 residui ka. Hoc idem fit in diametro gm portionis afce (quae parabola est). Nam gl habet 2/3 ipsius lm. Et ita centra parabolarum similiter dividunt suas diametros. Unde si centrum k alibi esset, sequeretur inconveniens.
17o novembris 1569.